on
모델링 - Michaelis - Menten과 Arrhenius eqn의 관계
모델링 - 지난 글
목차
효소반응 속도론이란
반응속도론(reaction kinetics)은 화학반응속도와 반응메커니즘에 대해 연구하는 학문분야이다. 반응속도론에서는 반응메커니즘, 반응속도에 영향을 미치는 반응물의 농도, 반응온도, pH 등과 같은 여러 가지 환경인자들에 대한 연구가 주요 대상이다.
광합성에서의 효소반응 속도
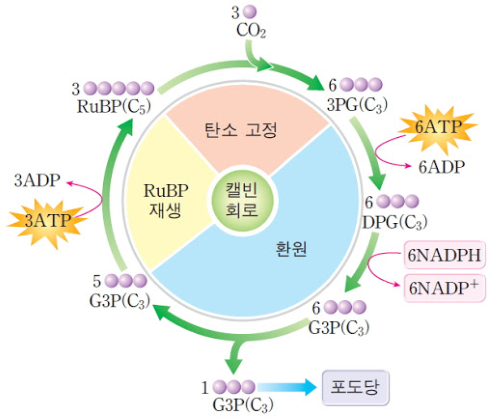캘빈 사이클
앞선 글에서 다음 캘빈 사이클에 대하여 간략하게 알아보았다. 캘빈 사이클은 스트로마에서 일어나며, 탄소(CO2)를 고정하고 포도당을 합성하고, 명반응의 결과 생성된 ATP와 NADPH를 이용하여 ADP와 NADP+를 내보내는 일련의 과정이 반복하는 사이클을 캘빈 사이클이라 한다고 하였다.
그렇다면 이번 시간에는 이를 더 깊게 파보겠다.
a) 캘빈회로는 주 효소인 Rubisco가 1mol의 이산화탄소를 RuBP 1mol에 고정시켜 2mol의 PGA를 만들어내며 시작된다. 이를 탄소고정 (carboxylation)이라 한다.
RuBP + CO2 + H2O → 2PGA
b) RuBP 1mol이 재생되는 데에 2mol의 PGA 및 NADPH 와 ATP로부터의 에너지가 필여하며, 또한 이 과정 중 각각 1mol의 탄수화물과 산소가 생성된다.
2PGA energy / (NADPH + ATP) → RuBP + CH2O + O2
Rubisco는 산소나 이산화탄소를 RuBP에 고정하는 반응을 모두 촉매하는 효소이다. 즉 이산화탄소와 산소가 RuBP를 두고 경쟁을 한다. 산소가 RuBP에 고정 (oxygenation)되는 과정이 광호흡이며 이를 통해 동화된 탄소의 10%가 손실되기 때문에 손해를 보는 과정이라 할 수 있다.
그리고 이러한 탄소 고정과 광호흡은 주변환경에 의해 결정된다. 식물이 있는 환경의 습도가 매우 낮아 건조하거나, 온도가 매우 높은 환경이라면 식물은 수분 손실을 막기 위해 기공을 닫을 것이다. 이때 기공을 통해서 오고가는 이산화탄소의 유입이 차단되면서 잎 내부는 이산화탄소 농도보다 산소의 농도가 더 높아질 것이다. 그리고 이런 상황에서 광호흡이 촉진된다.
즉, carboxylation과 oxygenation 반응은 온도 의존성이 큰 생화학 반응이며, 이 두가지 반응의 비는 주로 카르복실화가 일어나는 장소의 이산화탄소 및 산소 농도와 온도에 의해 결정된다.
Michaelis Menten
단일 기질-효소 촉매반응의 속도식은 Michaelis-Menten 속도식을 기본으로 한다. 효소속도론 의 정성적인 특징은 Langmuir-Hinshelwood 속도론과 비슷하다. 생물계에서는 다기질-다효 소반응과 같은 보다 복잡한 효소-기질간 상호작용이 일어날 수 있다. 효소는 기질과 결합할 수 있는 활성부위의 숫자가 일정하기 때문에 높은 기질농도에서는 활성부위 모두가 기질과 결합하 여 효소가 포화되는 상태가 된다.
효소 반응속도론은 다음과 같이 효소(E) - 기질(S)의 복합체(ES) 형성단계의 가역반응과 ES 복합체의 비가역 해리단계의 2단계의 반응체계로부터 구할 수 있다.
RuBP 탄소 및 산소 고정 과정
다음 자료는 RuBP 효소인 E가 carboxylation을 의미하는 ECMRC, oxygenation을 의미하는 ECMRO가 이루어지는 과정을 설명한다.
광합성 과정 중 암반응, 암반응 과정 중에서 탄소 고정반응의 Michaelis Menten 식은 다음과 같이 유도된다. 글로 설명하기에는 너무 복잡하니 다음
유튜브 링크를 통해서 이해하면 되겠다.
https://www.youtube.com/watch?v=iORGfGUtriM&list=LL&index=15&ab_channel=CHEMTOP%EC%BC%90%ED%83%91
| 표식 | 설명 | 단위 |
|---|---|---|
| Kc (25) | CO2에 대한 Michaelis-Menten 상수 | μmol/mol |
| Ko (25) | O2에 대한 Michaelis-Menten 상수 | μmol/mol |
| Vcmax (25) | Rubisco의 최대 carboxylation 속도 (엽면적당) | μmol/m2/s |
| Oa | 공기 중의 산소농도 | μmol/mol |
| Ci | 세포간극 공기 중 CO2 농고 (C3식물) | μmol/mol |
광합성 모델의 매개변수 값
여기서 Γ* 는 CO2 보상점이며 Ci = Γ* 에서 Vc = 0이 된다. 앞에서 언급했듯이 동화된 CO2의 일부는 광호흡을 통해서 손실 된다.
효소 반응속도의 온도 의존성
화학반응의 속도는 반응온도에 의해 영향을 받으며 대개 온도가 10℃ 상승하면 반응속도가 약 2배 증가하는 것으로 알려져 있다. 반응속도식에서 온도의 영향을 받는 인자는 식에서 기술한 바와 같이 반응속도 상수이다. 즉, 반응속도에 영향을 미치는 온도의 영향은 반응속도 상수(k) 의 온도의존성으로 나타낼 수 있다.
r = k(T )f (C i)
여기서 반응속도 상수의 온도의존성 k (T )는 일반적으로 아레니우스(Arrhenius) 식으로 표 현된다.
| 표식 | 설명 |
|---|---|
| K | 반응속도 상수 |
| A | 빈도 인자(frequency factor), k와 같은 단위를 가짐 |
| Ea | 활성화 에너지(activation energy, J/mol) |
| R | 기체상수(universal gas constant, 8.314 kJ/mol․K) |
| T | 절대온도 (K, 캘빈) |
Arrhenius eqn 매개변수
활성화 에너지
아레니우스(Arrhenius) 식은 비교적 넓은 온도범위에서 반응속도 상수의 온도의존성을 잘 나 타내며 온도가 증가할수록 반응속도 상수가 증가함을 나타낸다. 아레니우스 식에 들어 있는 활 성화 에너지 Ea 는 반응이 일어나기 위해서 반응물의 분자가 가져야 하는 최소에너지이다.
효소반응의 온도의존성
효소에 의한 촉매반응의 속도는 일정 한계까지 온도에 따라 증가하며 다른 화학반응과 마찬가 지로 아레니우스 식으로 표현할 수 있다. 그러나 효소반응은 다른 화학반응보다 온도 범위가 좁으며, 특정 온도 이상이 되면 단백질인 효소는 변성되어 온도가 증가하면 효소의 활성도는 오히려 감소한다.
일반적인 효소 촉매반응의 온도에 따른 변화
대체로 온도가 10 ℃씩 오를 때마다 효소반응의 속도는 약 두 배로 증가한 다. 기질과 효소의 분자운동이 증가하여 서로 접촉할 수 있는 기회가 늘어나기 때문 이다. 그러나 효소는 단백질이므로 열이 너무 많이 가해지면 형태가 변해서 제 기능을 못하 게 된다. 대부분의 경우 50～60 ℃ 이상의 온도에서는 효소의 활성도가 급격히 감소한다(그 림 8.12). 그러나 예외적으로 아주 높은 온도에서 잘 작용하는 효소도 있다. 예를 들어, 온천 지대에서 발견되는 미생물에는 내열성 효소가 존재한다.
배추모델에서의 효소반응 속도론과 반응속도의 온도 의존성 적용
##### Constants
KELVIN = 273.15 # Kelvin temperature
R = 8.314 # ideal gas constant
SBC = 5.6697e-8 # Stefan-Boltzmann constant W m-2 K-4
PSC = 6.66e-4 # psychrometer constant
Cp = 29.3 # specific heat of air J mol-1 C-1
LAMBDA = 44000. # Latent heat of vaporization at 25 C J mol-1
##### Parameters for light
scatt = 0.15 # leaf reflectance + transmittance
f = 0.15 # correction factor
conv = 4.57 # conversion from W m-2 to umol m-2 s-1
epsilon = 0.97 # leaf thermal emissivity
##### Other Common parameters
O2 = 210. # O2 partial pressure (mbar=20.5kPa)
Kc25 = 404.9 # MM constant of Rubisco for CO2 at 25 from Bernacchi et al. (2001)
Ko25 = 278.4 # MM constant of Rubisco for O2 at 25 from Bernacchi et al. (2001)
Eac = 79430. # Activation energy for Kc from Bernacchi et al. (2001)
Eao = 36380. # Activation energy for Ko from Bernacchi et al. (2001)
g0 = 0.036 # residual stomatal conductance, mol m-2 s-1
g1 = 10.0 # empirical coefficient of BWB model 이거
P = 1.013 # conversion factor from ppmv to ubar (= 1013000 / 1000000) = 101.3 kPa = 1013 mbar
##########################################################
##### Parameters for Chinese cabbage from Experiment 2015
##########################################################
theta = 0.7 # hyperbola parameter 이거
width = 0.1 # leaf width (m) 이거
Vcm25 = 152.5 # Vcmax of CC at 25 C 이거
Jm25 = 238.6 # Jmax of CC at 25 C 이거
TPU25 = 17.1 # 이거
Rd25 = 1.7 # 이거
gamma25 = 42.8 #
Havcm = 65330 # Ha
# Hdvcm = 149252. # Hd
# Svvcm = 486. # Sv
Hajm = 57500 # Ha
Hdjm = 439800. # Hd
Svjm = 1400 # Sv
Ear = 46390. # Ha
Eagamma = 37830. # Ha
EaTPU = 47100. # Ha for TPU from Kim and Leith(2003)
Michaelis Menten 상수를 포함하여, Arrhenius 매개변수 정의
def calcParam(self):
temp = self.Ta
Vcmax = self.tempParam2(k25=Vcm25, Ha=Havcm, temp=temp) # , Hd=Hdvcm, Sv=Svvcm, temp=temp)
Jmax = self.tempParam1(k25=Jm25, Ha=Hajm, Hd=Hdjm, Sv=Svjm, temp=temp)
GammaStar = self.tempParam2(k25=gamma25, Ha=Eagamma, temp=temp)
# print(GammaStar)
Kc = self.tempParam2(k25=Kc25, Ha=Eac, temp=temp)
Ko = self.tempParam2(k25=Ko25, Ha=Eao, temp=temp)
TPU = self.tempParam2(k25=TPU25, Ha=EaTPU, temp=temp)
Rd = self.tempParam2(k25=Rd25, Ha=Ear, temp=temp)
self.Vcmax = Vcmax # rubisco
self.Jmax = Jmax # RuBP
self.GammaStar = GammaStar #
self.TPU = TPU
self.Kc = Kc
self.Ko = Ko
self.Rd = Rd
def tempParam1(self, k25, Ha, Hd, Sv, temp):
a = (1 + np.exp((Sv * (25 + KELVIN) - Hd) / (R * (25 + KELVIN)))) / (
1 + np.exp((Sv * (temp + KELVIN) - Hd) / (R * (temp + KELVIN))))
b = np.exp((Ha / (R * (25. + KELVIN))) * (1 - (25. + KELVIN) / (temp + KELVIN)))
return (k25 * b * a)
def tempParam2(self, k25, Ha, temp):
return k25 * np.exp(
(Ha / (R * (25. + KELVIN)) * (1 - (25. + KELVIN) / (KELVIN + temp)))) # --> arrhenius function
효소반응의 온도의존성을 설명하는 Arrhenius eqn을 수식으로 정의