Written by Seungwon Seok
on 
모델링 - 파이썬으로 FvCB A-Ci 커브 그려보기
FvCB 기반 Co2에 따른 엽단위 광합성량을 구하고 시각화 해보기.


모델링 - 지난 글

목차

  1. 광합성에 대하여
  2. FvCB는 무엇인가?
  3. 광합성량을 구하기 위한 수식
  4. Co2에 따른 광합성량 구하고 시각화하기


광합성에 대하여

광합성은 식물이 성장하기 위한 영양소를 만들어 내는 과정이라는 사실은 모두가 알고 있을 것이다. 조금 더 자세히 이야기 해 보도록 하자.

식물의 잎이 녹색으로 보이는 이유는 식물 잎 세포의 엽록체에 포함된 엽록소가 녹색 파장의 빛을 반사시키고 파란색과 붉은색 파장의 빛을 주로 흡수하기 때문이다. 녹색식물은 이렇게 태양으로부터 얻은 빛에너지를 이용하여 뿌리에서 흡수한 물, 잎의 기공을 통해 흡수한 이산화탄소를 재료로 하여 당류나 전분과 같은 탄수화물을 합성하는 탄소동화작용을 한다. 이와 같이 탄소동화작용이 고등식물에서 볼 수 있는 바와 같이 빛에너지에 의존하는 경우에 이를 광합성(photosynthesis)이라 한다.

광합성에 의해 만들어진 탄수화물이나 그밖에 변해서 생긴 여러 가지 유기물질 즉, 넓은 의미의 동화 생산물은 높은 화학적 에너지를 간직하고 있으므로 광합성은 태양의 빛에너지를 화학에너지로 바꾸어 식물체 내에 축적하는 과정이라 할 수 있다. 광합성의 결과 포도당을 포함한 6탄당과 전분이 만들어지며 주로 포도당이 주로 생성되기 때문에 광합성을 나타내는 반응식은 흔히 다음과 같이 나타낸다.

6CO2 + 12H2O + 빛 에너지 → C6H12O6 + 6H2O + 6O2 – 688kcal


광합성 과정

광합성에는 명반응과 암반응 두 단계로 진행된다.

명반응

암반응

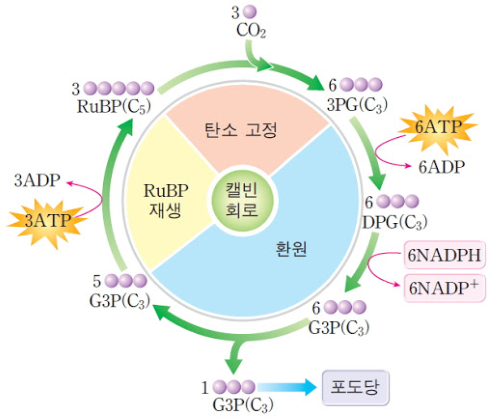
정리하자면 명반응으로 부터 생성된 ATP와 NADPH을 에너지로 삼아 암반응에서 포도당을 생성할 수 있고, 암반응을 통해서 만들어진 ADP와 NADP+가 있어야 명반응이 계속해서 이루어 질 수 있다.

fvcb는 무엇인가


광합성량을 구하기 위한 수식

Ac, Aj, Ap는 캘빈 사이클 내의 연속 구성 요소이기 때문에 가장 속도를 제한하는 프로세스가 순 광합성 속도를 결정할 것이다. (최소율의 법칙)

각 프로세스의 속도는 효소의 특성 뿐만 아니라 온도, 빛, Co2 및 O2와 같은 환경변수에 반응한다.

Ac

Aj

J는 Jmax, Iabs, aLL 하에서의 전자 수송의 양자 수율. J에서 Iabs 응답 곡선의 볼록성을 나타내는 경험적 (empirical) 매개변수 Θ (theta)에 의존

Ap


co2에 따른 광합성량 구하고 시각화하기

위의 수식을 활용해서 임의의 조건에서의 A-Ci 커브를 그려보자.

파이썬을 이용한 광합성 모델

import matplotlib.pyplot as plt
import numpy as np



##### Constants
KELVIN   = 273.15       # Kelvin temperature
R        = 8.314        # ideal gas constant
SBC      = 5.6697e-8    # Stefan-Boltzmann constant   W m-2 K-4
PSC      = 6.66e-4      # psychrometer constant
Cp       = 29.3         # specific heat of air    J mol-1 C-1
LAMBDA   = 44000.       # Latent heat of vaporization at 25 C J mol-1
##### Parameters for light
scatt   = 0.15          # leaf reflectance + transmittance
f       = 0.15          # correction factor
conv    = 4.57          # conversion from W m-2 to umol m-2 s-1
epsilon = 0.97          # leaf thermal emissivity
##### Other Common parameters
O2    = 210.            # O2 partial pressure (mbar=20.5kPa)
Kc25  = 404.9           # MM constant of Rubisco for CO2 at 25 from Bernacchi et al. (2001)
Ko25  = 278.4           # MM constant of Rubisco for O2 at 25 from Bernacchi et al. (2001)
Eac   = 79430.  # Activation energy for Kc from Bernacchi et al. (2001)
Eao   = 36380.  # Activation energy for Ko from Bernacchi et al. (2001)
g0    = 0.036    # residual stomatal conductance,  mol m-2 s-1
g1    = 10.0    # empirical coefficient of BWB model  이거
P     = 1.013   # conversion factor from ppmv to ubar (= 1013000 / 1000000) = 101.3 kPa = 1013 mbar

##########################################################
##### Parameters for Chinese cabbage from Experiment 2015
##########################################################
theta   = 0.7       # hyperbola parameter 이거
width   = 0.1        # leaf width (m) 이거
Vcm25   = 152.5     # Vcmax of CC at 25 C 이거
Jm25    = 238.6      # Jmax  of CC at 25 C 이거
TPU25   = 17.1       # 이거F
Rd25    = 1.7        # 이거
gamma25 = 42.8        #
Havcm   = 65330     # Ha
Hajm    = 57500     # Ha
Hdjm    = 439800.    # Hd
Svjm    = 1400      # Sv
Ear     = 46390.     # Ha
Eagamma = 37830.     # Ha
EaTPU   = 47100.     # Ha for TPU   from Kim and Leith(2003)



Ta = 25      # 온도 고정
Ic = 2000    # 광량 고정

Cinew = []   # 잎 내 Co2 농도

for i in range(1,1500):
    Cinew.append(i)

def tempParam1(k25, Ha, Hd, Sv, temp):
    a = (1+np.exp((Sv*(25+KELVIN)-Hd)/(R*(25+KELVIN))))/(1+np.exp((Sv*(temp+KELVIN)- Hd)/(R*(temp+KELVIN))))
    b = np.exp((Ha / (R * (25.+KELVIN))) * (1 - (25.+KELVIN) / (temp + KELVIN)))
    return (k25 * b * a)

def tempParam2(k25, Ha, temp):
    return  k25 * np.exp((Ha / (R * (25.+KELVIN)) * (1 - (25.+KELVIN) / (KELVIN + temp)))) # --> arrhenius function


Vcmax = tempParam2(k25=Vcm25, Ha=Havcm, temp=Ta)
Jmax = tempParam1(k25=Jm25, Ha=Hajm, Hd=Hdjm, Sv=Svjm, temp=Ta)
GammaStar = tempParam2(k25=gamma25, Ha=Eagamma, temp=Ta)
Kc = tempParam2(k25=Kc25, Ha=Eac, temp=Ta)
Ko = tempParam2(k25=Ko25, Ha=Eao, temp=Ta)
TPU = tempParam2(k25=TPU25, Ha=EaTPU, temp=Ta)
Rd = tempParam2(k25=Rd25, Ha=Ear, temp=Ta)



J2 = Ic * (1 - scatt) * (1 - f) / 2
J = ((J2 + Jmax) - np.sqrt((J2 + Jmax) ** 2 - 4 * J2 * Jmax * theta)) / (2 * theta)



## 광합성 모델식
Wc = []
Wj = []
Ws = []
Wp = []
W=[]
Rd = []
An = []
W_net = []

def minh(A, B, theta=0.7):  # hyperbolic minimum
    x = (A + B) * (A + B) - 4 * A * B * theta
    if (x < 0):
        res = min(A, B)
    else:
        res = ((A + B) - np.sqrt(x)) / (2 * theta)
    return res

for i in range(len(Cinew)):
    Wc.append(Vcmax * (Cinew[i] - GammaStar) / (Cinew[i] + Kc * (1 + O2 / Ko)))  # Rubisco-limited
    Wj.append(J * (Cinew[i] - GammaStar) / (4 * (Cinew[i] + 2 * GammaStar)))
    Ws.append(3 * TPU)
    Wp.append(minh(Wc[i], Wj[i], theta))
    W_net.append(min(Wc[i],Wj[i],Ws[i]))
    W.append(min(Wp[i], Ws[i]))  # min(Wp, Ws)
    Rd.append(0.015 * Vcmax)  # Dark respiration from Collatz(1991)
    An.append(W[i] - Rd)

시각화

25°C


10°C


45°C


참고 문헌

다음 시간에는 Michaelis - Menten과 Arrhenius equation에 대하여 자세히 다루어 보자.